AXIAL & ORBITAL ROTATIONS
Galactic Magnetic Field Influences Orbits
Axial and Orbital Rotations
© Charles Chandler
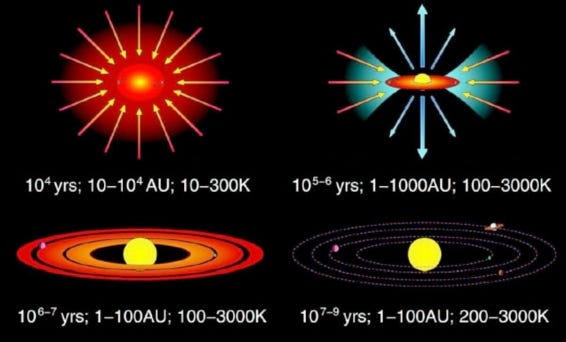
In the standard model, the planets in our solar system formed from the same accretion disc as the Sun. (See Figure 1.)
Figure 1. Standard model of stellar and planetary formation, credit Shu et al. (1987).
© 1987 NASA
This would seem to explain why all of the planets orbit the Sun in the same direction that the Sun rotates on its axis, if all of it condensed from the same disc, and if the disc was rotating.
But this doesn't explain why all of the rotations that we can detect, including the orbits within our solar system, and the rotations of planetary nebulae, are aligned to the external magnetic fields, far beyond chance.1,2,3,4 This suggests that the particles involved in the radial implosion were charged, and thus developed a spin due to the Lorentz force. The galactic magnetic field is extremely weak, and yet the total angular momentum in the solar system is extremely small, given the size of the dusty plasma from which it condensed. An extremely weak force, acting on matter over a long period of time, traveling a great distance, can certainly induce a small rotation.
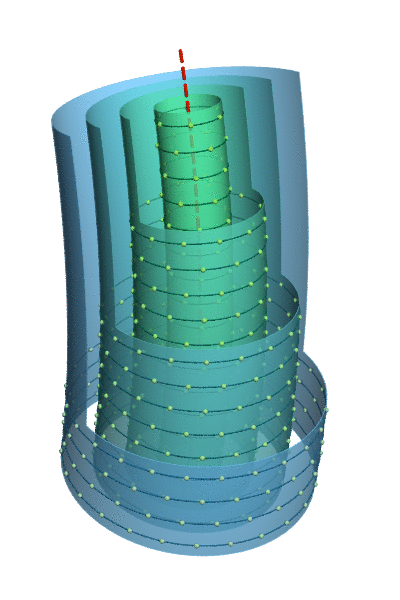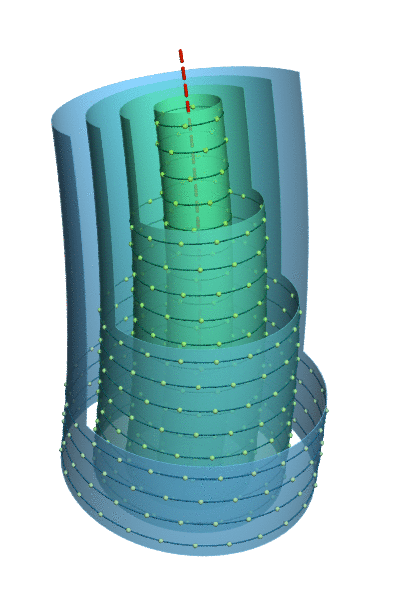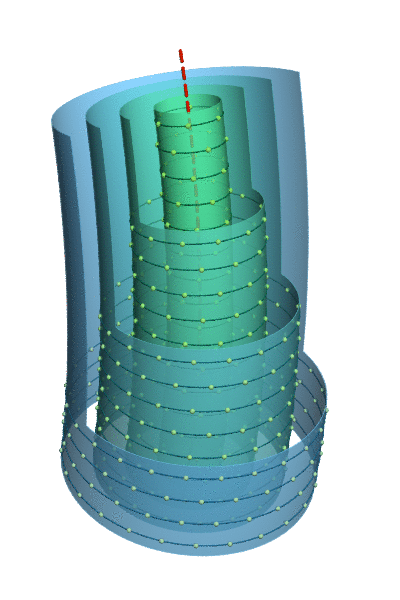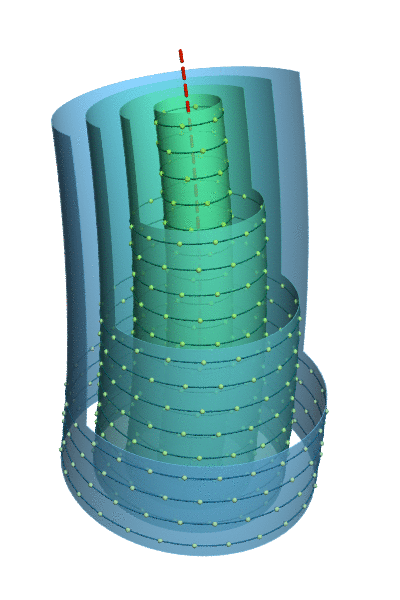
Figure 2. Angular velocities in a free vortex, courtesy Jorge Stolfi.
This also explains the predominantly prograde axial spins in our solar system, which the standard model cannot. To think that planets would rotate on their axes in the same direction that they rotate around the Sun, for the same reason, is naïve, and if we take a close look at the actual forces involved, we find that Newtonian forces should dictate retrograde axial spins. Angular velocities increase with proximity to the axis of rotation. (See Figure 2.) This means that if all of the matter within a strip of the disc condenses, the net angular momentum within that strip is retrograde. For example, the general rotation in Figure 2 is counter-clockwise in top view. But if all of the particles within the extents of the three outer shells condensed into one body, that body would rotate clockwise (i.e., retrograde), since the left shoulder (i.e., the inner matter) will be traveling faster than the right shoulder (i.e., the outer matter), facing in the direction of the orbital rotation. This left/right momentum should be quite respectable, and the same weak Lorentz force that induced the overall rotation shouldn't be capable of overpowering it. This makes it difficult to image how the planets condensed from strips within the accretion disc. It's easier to believe that irregularities in the collapsing dusty plasma meant that not all of it collapsed on precisely the same point. Rather, there were multiple nuclei of condensation. The matter converging on each of these points will have angular momenta, in the same direction, and for the same reason, but each as a separate instance, not as components of a single system.
Then there is the exception that proves the rule. The one planet that does have a retrograde axial rotation (i.e., Venus) is slowing down. Without any moons, tidal forces are weak, and thus tidal friction cannot account for the loss of angular momentum. Friction from atmospheric winds cannot be the cause, since they are retrograde as well, and rotate much faster than the solid surface, so they should speed up the retrograde rotation. This can only mean that there is another force, which can only be the external magnetic field. So the same Lorentz force that induced the rotation in the first place is still at work.
Figure 3. Jupiter
Note that for the external magnetic field to have any effect on the axial rotation of a planet, the planet has to have a net charge. This, of course, is problematic, since there is no reason to believe that a planet could sustain a net charge for any length of time, in the absence of sufficient resistance. Yet there is a way for a net neutral planet to act as if it has a net charge. If the planet is made up of current-free double-layers (CFDLs), the charges might all be in equilibrium, but the outer layer will have more torque. On Venus, when we see that the atmosphere's retrograde rotation is currently getting accelerated, while the solid sphere's rotation is getting decelerated, we can conclude that it's the same force at work in both cases, but the atmosphere has a different charge from the solid surface. So the Lorentz force sends oppositely charged layers in opposite directions. Similarly, when we observe counter-rotating bands in the atmosphere of Jupiter (as in Figure 3), these can only be oppositely charged chemicals accelerated in a magnetic field.
More Issues to Explore
axial and orbital precession
What if the Earth's precession is a consequence of the event that put the Moon into orbit around the Earth? My working hypothesis is that the Moon was the impactor, while Celeste is talking about a perfect near miss of a much larger body, which created a tidal bulge that split off to form the Moon. Either way, if the force applied to the Earth wasn't perfectly in line with the Earth's existing rotation, precession would have resulted.
Another possibility is that the galactic magnetic field is not perpendicular to the plane of orbital rotation. I like that better than my axial magnetic conflict idea for precession, because the latter doesn't explain why other planets don't precess.
correlation between orbital inclination and aspect ratio of elliptical orbit (the ellipses projected onto the invariable plane are all circles)
Bode's Law
Orbits of planets increase at a regular rate.
Charles Chandler: electrostatic/gravitational equilibrium
Chad Glass: electrical resonance
The orbits and prograde rotations are cloned signals in sympathetic electrical resonance with the parent star (Sun). Realize that per spiraling helix oribts these are actually sine waves. These sine waves are electrically induced and overridden/established by the Sun as the primary node of the signal. Orbits, then, are ancillary and/or cloned facsimiles of the Sun's dominating electrical wave envelope. The Sun induces a literal dance of the particles around it.
Once a planet is born of and/or enters the Sun's plasma envelope, the body encounters the influence of the Sun's signal profile that is physically expressed in its rotation--the Sun being a rotating generator or motor. You could also consider it to be a voltage regulator and virtual cathode. This electrical device, the Sun, can be measured on an oscilloscope in all likelihood. This may also tie into why planets tend to "quantize" into a Titus Bode relationship. They are self-arranging as they are "signal cloned" into sympathetic positions very much like notes in a musical scale. It may also have to do with harmonics. Things will tend to vibrate and assume the waveform of adjacent dominant signals, ripples.
rotation of entire solar system (either because the Sun is in a long period rotation with a binary companion, or because it is moving in a helical path through the spiral arm magnetic field)
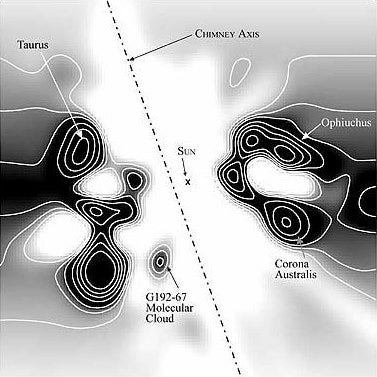
Figure 4. Local Chimney
© 2003 UC Berkeley
Figure 5. Milky Way in Infrared The diagonal blue band is dust in the plane of the solar system.
© 2017 CalTech
Another factor to consider concerning the rotation of the Sun is that it is perpendicular to the Local Chimney. (See Figure 4 and Figure 5.) If the Sun formed from a linear filament, its axis of rotation would be perpendicular to the axis of the filament.
References
1. Gaensler, B. M. (1999): Morphological Studies of Extragalactic Supernova Remnants. Perspectives on Radio Astronomy: Science with Large Antenna Arrays, 271-274 ⇧
2. Bhatnagar, S. (2001): Radio Study of Galactic Supernova Remnants and the Interstellar Medium. Tata Institute of Fundamental Research, Pune, India ⇧
3. Henning, T.; Li, H. (2011): The alignment of molecular cloud magnetic fields with the spiral arms in M33. Nature, 479 (7374): 499-501 ⇧
4. Beck, R. (2000): Magnetic fields in normal galaxies. Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 358 (1767): 777-796 ⇧
CFDLs Caused by EDP
© Charles Chandler
Figure 1. Charge Separation Under Pressure
Scheme of the electric charge separation induced by the ponderomotive force in the wake of the laser pulse, [D'Amico 07a]. {Charles’ illustration is no longer available, so I used the one above, which gives the general idea. Charles’ original caption is the following paragraph.}
{Quote:} At left is an abstract representation of a normal crystal lattice, using the familiar icon for an atom, and showing connections of electron shells. At right, extreme pressure has forced the expulsion of one of the electrons from the atom in the center. The expelled electron is to be found just outside, wherever there is room for it, while attracted to the positive ion by the electric force. {End quote.}
It is well-known that at high pressures, matter gets ionized.1 This is because of the Pauli Exclusion Principle, whereby no two identical fermions (i.e., particles with half-integer spins, such as electrons) may simultaneously occupy the same quantum state in the same location. If atoms are pressed too close together, the electron shells of neighboring atoms overlap, and the conflict forces the liberation of one of the electrons. The extra force required to do this accounts for the incompressibility of liquids and solids.2,3,4 (See Figure 1.)
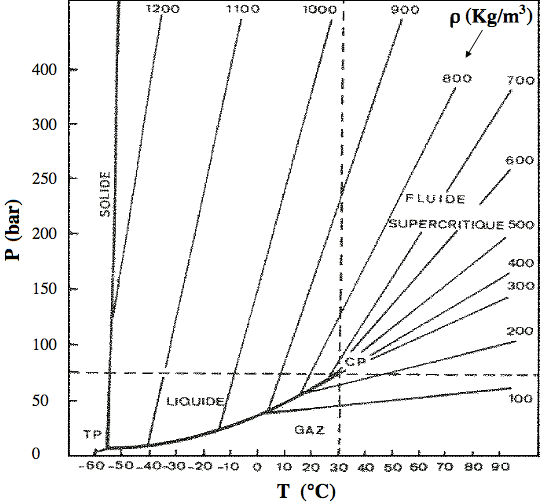
The same is true even for supercritical fluids — even though they're too hot for crystal lattices, and thus have a plasticity uncharacteristic of their subcritical solid regimes, once compressed down to the density of a solid, they become just as incompressible as subcritical solids.5,6 This fact isn't salient in the larger body of studies that have been done on supercritical fluids at less extreme pressures, and there's actually one place in the phase diagram where supercritical fluids are compressible beyond even the ideal gas laws — just above the critical temperature. (See the Nelson-Obert charts, and the closely spaced density lines just above the CP in Figure 2.) Nevertheless, the fluid is as incompressible as ever once it achieves its solid density. (See Figure 3.) CO2 at its critical temperature of 31 °C, when subjected to 300 GPa (i.e., 3 million bars), has a density of 1400 kg/m3, which isn't much above its solid density below the triple point. So supercritical fluids still have a modulus of elasticity beginning at the solid density, but that isn't what we'd call compressibility, certainly not in line with the ideal gas laws.
Figure 2. Carbon dioxide phase diagram.
© 2000 FutureChem
Figure 3. Another representation of the density of the various states.7 In the solid regime, increasing pressure doesn't further compress the matter — it simply enables the closest packed arrangement even at increasing temperatures.
Thus the Pauli Exclusion Principle holds even for supercritical fluids. Monoatomic matter above the critical point isn't constrained by covalent bonds. But when two atoms are forcibly pushed together, the first conflict will be between the outer electrons. If the pressure is greater than the ionization potential of the atoms, the conflict results in the expulsion of electrons, leaving a strong electrostatic repulsion between the positively charged atomic nuclei, and further compression has to fight the Coulomb force. This marks the transition from compressibility to elasticity, which is very different. The Quantum Mechanics term for this effect is electron degeneracy pressure (EDP), though the Pauli Exclusion Principle predated QM, and is not reliant on it.
If the pressure is coming from gravitational loading, it increases with depth, meaning greater compression, and atoms packed closer together. At the threshold for EDP, electrons are expelled, and they have nowhere to go but up, where they will find room between atoms that aren't as tightly packed. Thus the expelled electrons are forced to a higher altitude, leaving positive ions below.
The implication not typically considered is that a charge separation has occurred, creating current-free double-layers (CFDLs) — they are layers of opposite charges, with a powerful electric field between them, but there is no current responding to the field, because something prevents it. Usually a sustained charge separation requires an insulator, but in this case, EDP separates the charges and keeps them separate. And gravity is forcing the EDP. So as long as those forces are present, there will be a charge separation, and an electric field.
References
1. Saumon, D.; Chabrier, G. (1992): Fluid hydrogen at high density: Pressure ionization. Physical Review A, 46 (4): 2084-2100 ⇧
2. Dyson, F. J.; Lenard, A. (1967): Stability of Matter. I. Journal of Mathematical Physics, 8 (3): 423-434 ⇧
3. Lenard, A.; Dyson, F. J. (1968): Stability of Matter. II. Journal of Mathematical Physics, 9 (5): 698-711 ⇧
4. Dyson, F. J. (1967): Ground‐State Energy of a Finite System of Charged Particles. Journal of Mathematical Physics, 8 (8): 1538-1545 ⇧
5. Otles, S. (2016): Supercritical Fluids — Density Considerations. ⇧
6. Tosatti, E. et al. (2009): High-pressure polymeric phases of carbon dioxide. Proceedings of the National Academy of Sciences, 106 (15): 6077-6081 ⇧
7. Weill, F. et al. (1999): Supercritical fluid processing: a new route for materials synthesis. Journal of Materials Chemistry, 9 (1): 67-75 ⇧
Nelson_Obert_Chart.png
Nelson-Obert chart, courtesy San Diego State University. When Tr = 1.00, the temperature is at the critical point, and the compressibility decreases rapidly with increasing pressure. This is the incompressibility of liquids. But above the critical pressure (Pr = 1.00), the plasma is more compressible than predicted by the ideal gas laws, especially at the lower temperatures.